RESEARCH

Keywords:
Sparse Learning, Predictive Modeling, Feature Selection, Bayesian Inference, Monte Carlo, Dynamical Systems, Deep Learning, Real Data Applications

General

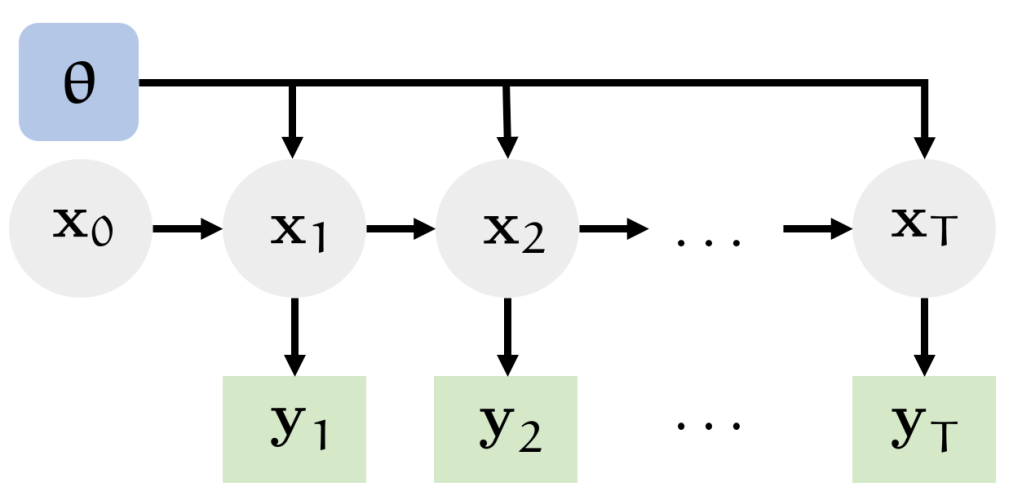
In PhD my research, I focused on developing models and algorithms that predict the outcomes of a dynamical system such as a moving object, a chemical reaction, populations of species, and in general, any system which evolves over time. To do this, we need to learn the inner workings of the system. Measurements such as position and speed, concentration of a chemical, and population counts at a local site, are taken and used to estimate (infer) some parameter values of the models that describe the observed phenomena. These parameters are inherent to the system and are crucial in explaining what is observed.  Examples of parameters include reaction rate constants, gravity, and breeding propensity. Unlike in the case of gravity, parameters which describe these systems are not always known.

More technically, my research revolves around two main objectives: i) estimation and prediction of the hidden processes in a dynamical system (the latent states), and ii) estimation of the connections between the latent states in the system (the network and its topology), given time-series data. While a number of challenges exist when employing Bayesian inference for such systems, the ones of main concern in my focus are scalability and online inference.